이전 글(선형 검색)
2022.11.27 - [Code/Algorithm] - [Algorithm] 검색 알고리즘_2 (선형 검색)
[Algorithm] 검색 알고리즘_2 (선형 검색)
03-2 선형 검색 선형 검색(linear search) 직선 모양(선형)으로 늘어선 배열에서 검색하는 경우에 원하는 키값을 가진 원소를 찾을 때까지 맨 앞부터 스캔하여 순서대로 검색하는 알고리즘 선형 검색
heejins.tistory.com
03-3 이진 검색
이진 검색(binary search)
- 원소가 오름차순이나 내림차순으로 정렬된 배열에서 좀 더 효율적으로 검색할 수 있는 알고리즘
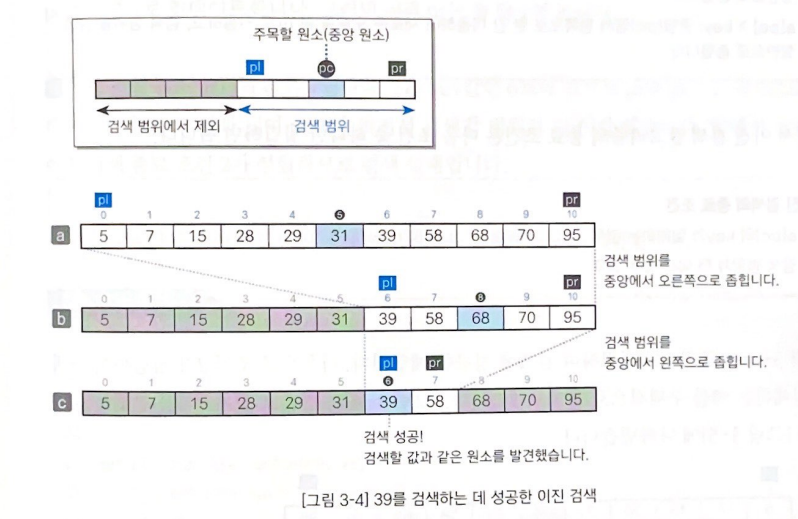
검색 범위는 흰색 배열 안의 원소이고, 검색에서 제외되는 범위는 회색 배열 안의 원소입니다. 이진 검색을 한 단계씩 진행할 때마다 검색 범위는 거의 반으로 좁혀집니다. 또한 주목할 원소를 하나씩 차례대로 이동하는 선형 검색과 달리, 이진 검색에서는 주목할 원소를 다음에 검색할 범위의 중간 지점으로 단숨에 이동합니다.
위 그림의 c처럼 a[pc]와 key(찾아야할 값)를 비교하여 같으면 검색에 성공한 것입니다. 하지만 key를 찾지 못하면 다음과 같은 방법으로 검색 범위를 좁힐 수 있습니다.
이진 검색의 종료 조건
- a[pc]와 key가 일치하는 경우
- 검색 범위가 더 이상 없는 경우
실습 3-4 이진 검색 알고리즘
# 이진 검색 알고리즘
from typing import Any, Sequence
def bin_search(a: Sequence, key: Any) -> int:
"""시퀀스 a에서 key와 일치하는 원소를 이진 검색"""
pl = 0 # 검색 범위 맨 앞 원소의 인덱스
pr = len(a) -1 # 검색 범위 맨 끝 원소의 인덱스
while True:
pc = (pl + pr) // 2 # 중앙 원소의 인덱스
if a[pc] == key:
return pc # 검색 성공
elif a[pc] < key:
pl = pc + 1 # 검색 범위를 뒤쪽 절반으로 좁힘
else:
pr = pc -1 # 검색 범위를 앞쪽 절반으로 좁힘
if pl > pr:
break
return -1 # 검색 실패
if __name__ == '__main__':
num = int(input('원소 수를 입력하세요.: '))
x = [None] * num # 원소 수가 num인 배열을 생성
print('배열 데이터를 오름차순으로 입력하세요.')
x[0] = int(input('x[0]: '))
for i in range(1, num):
while True:
x[i] = int(input(f'x[{i}]: '))
if x[i] >= x[i -1]: # 바로 직전에 입력한 원솟값보다 큰 값을 입력
break
ky = int(input('검색할 값을 입력하세요.: ')) # 검색할 키값 ky를 입력
idx = bin_search(x, ky) # ky값과 같은 원소를 x에서 검색
if idx == -1:
print('검색값을 갖는 원소가 존재하지 않습니다.')
else:
print(f'검색값은 x[{idx}]에 있습니다.')원소 수를 입력하세요.: 4
배열 데이터를 오름차순으로 입력하세요.
x[0]: 5
x[1]: 9
x[2]: 10
x[3]: 25
검색할 값을 입력하세요.: 9
검색값은 x[1]에 있습니다.복잡도(complexity)
- 복잡도: 프로그램의 실행 속도(또는 실행하는 데 필요한 시간)는 프로그램이 동작하는 하드웨어나 컴파일러 등의 조건에 따라 달라집니다. 알고리즘의 성능을 객관적으로 평가하는 기준을 복잡도(complexity)라고 합니다.
- 시간 복잡도(time complexity): 실행하는 데 필요한 시간을 평가합니다.
- 공간 복잡도(space complexity): 메모리(기억 공간)와 파일 공간이 얼마나 필요한지를 평가합니다.
선형 검색의 시간 복잡도
def seq_search(a: Sequence, key: Any) -> int:
i = 0 # 1
while i < n : # 2
if a[i] == key: # 3
return i # 4 검색에 성공하여 인덱스를 반환
i += 1 # 5
return -1 # 6 검색에 실패하여 -1을 반환선형 검색 단계별 실행 횟수와 복잡도
| 단계 | 실행 횟수 | 복잡도 |
| 1 | 1 | O(1) |
| 2 | n / 2 | O(n) |
| 3 | n / 2 | O(n) |
| 4 | 1 | O(1) |
| 5 | n / 2 | O(n) |
| 6 | 1 | O(1) |
n이 점점 커지면 O(n)에 필요한 계산 시간은 n에 비례하여 점점 길어집니다. 하지만 O(1)에 필요한 계산 시간은 변하지 않습니다. 여기에서 짐작할 수 있듯이 O(f(n))과 O(g(n))의 동작을 연속으로 하는 경우 복잡도는 일반적으로 다음과 같이 나타냅니다.
O(f(n)) + O(g(n)) = O(max(f(n), g(n)))
2가지 계산으로 구성된 알고리즘의 복잡도는 차원이 더 높은 쪽의 복잡도를 우선으로 합니다. 3가지 이상의 계산으로 구성된 알고리즘도 마찬가지입니다. 다시 말해 전체 복잡도는 차원이 가장 높은 복잡도를 선택하는 격입니다. 그러므로 선형 검색 알고리즘의 복잡도는 다음과 같이 O(n)이 됩니다.
O(1) + O(n) + O(n) + O(1) + O(n) + O(1) = O(max(1, n, n, 1, n, 1)) = O(n)
이진 검색의 시간 복잡도
def bin_search(a: Sequence, key: Any) -> int:
"""시퀀스 a에서 key와 일치하는 원소를 이진 검색"""
pl = 0 # 1 검색 범위 맨 앞 원소의 인덱스
pr = len(a) -1 # 2 검색 범위 맨 끝 원소의 인덱스
while True:
pc = (pl + pr) // 2 # 3 중앙 원소의 인덱스
if a[pc] == key: # 4
return pc # 5 검색 성공
elif a[pc] < key:: # 6
pl = pc + 1 # 7 검색 범위를 뒤쪽 절반으로 좁힘
else:
pr = pc -1 # 8 검색 범위를 앞쪽 절반으로 좁힘
if pl > pr:: # 9
break
return -1 # 10 검색 실패| 단계 | 실행 횟수 | 복잡도 |
| 1 | 1 | O(1) |
| 2 | 1 | O(1) |
| 3 | log n | O(log n) |
| 4 | log n | O(log n) |
| 5 | 1 | O(1) |
| 6 | log n | O(log n) |
| 7 | log n | O(log n) |
| 8 | log n | O(log n) |
| 9 | log n | O(log n) |
| 10 | 1 | O(1) |
이진 검색 알고리즘의 ㅂ고잡도는 다음과 같이 O(log n)으로 얻을 수 있습니다.
O(1) + O(1) + O(log n) + O(log n) + O(1) + O(log n) + ··· + O(1) = O(log n)
실습 3C-3 이진 검색 알고리즘의 실행 과정을 출력
# 이진 검색 알고리즘의 실행 과정을 출력
from typing import Any, Sequence
def bin_search(a: Sequence, key: Any) -> int:
"""시퀀스 a에서 key와 일치하는 원소를 이진 검색(실행 과정을 출력)"""
pl = 0 # 검색 범위 맨 앞 원소의 인덱스
pr = len(a) -1 # 검색 범위 맨 끝 원소의 인덱스
print(' |', end='')
for i in range(len(a)):
print(f'{i:4}',end='')
print()
print('---+' + (4*len(a) + 2) * '-')
while True:
pc = (pl + pr) // 2 # 중앙 원소의 인덱스
print(' |', end='')
if pl != pc:
print((pl *4 + 1) * ' '+ '<-' + ((pc-pl) * 4) * ' '+ '+',end='')
else:
print((pc * 4 + 1) * ' ' + '<+',end='')
if pc != pr:
print(((pr - pc)* 4 -2) * ' '+ '->')
else:
print('->')
print(f'{pc:3}|', end='')
for i in range(len(a)):
print(f'{a[i]:4}',end='')
print('\n |')
if a[pc] == key:
return pc # 검색 성공
elif a[pc] < key:
pl = pc + 1 # 검색 범위를 뒤쪽 절반으로 좁힘
else:
pr = pc -1 # 검색 범위를 앞쪽 절반으로 좁힘
if pl > pr:
break
return -1 # 검색 실패
if __name__ == '__main__':
num = int(input('원소 수를 입력하세요.: '))
x = [None] * num # 원소 수가 num인 배열을 생성
print('배열 데이터를 오름차순으로 입력하세요.')
x[0] = int(input('x[0]: '))
for i in range(1, num):
while True:
x[i] = int(input(f'x[{i}]: '))
if x[i] >= x[i -1]: # 바로 직전에 입력한 원솟값보다 큰 값을 입력
break
ky = int(input('검색할 값을 입력하세요.: ')) # 검색할 키값 ky를 입력
idx = bin_search(x, ky) # ky값과 같은 원소를 x에서 검색
if idx == -1:
print('검색값을 갖는 원소가 존재하지 않습니다.')
else:
print(f'검색값은 x[{idx}]에 있습니다.')원소 수를 입력하세요.: 5
배열 데이터를 오름차순으로 입력하세요.
x[0]: 3
x[1]: 5
x[2]: 6
x[3]: 10
x[4]: 30
검색할 값을 입력하세요.: 10
| 0 1 2 3 4
---+----------------------
| <- + ->
2| 3 5 6 10 30
|
검색값을 갖는 원소가 존재하지 않습니다.- 출처: Do it! 자료구조와 함께 배우는 알고리즘 입문 - 파이썬 편
- notebook ipynb file: https://github.com/heejvely/Algorithm/blob/main/Do_it_algorithm/Do_it_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98_%EA%B2%80%EC%83%89%20%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98.ipynb
GitHub - heejvely/Algorithm: 파이썬 알고리즘 인터뷰 책을 참고한 파이썬 알고리즘 연습
파이썬 알고리즘 인터뷰 책을 참고한 파이썬 알고리즘 연습. Contribute to heejvely/Algorithm development by creating an account on GitHub.
github.com
'Code > Algorithm' 카테고리의 다른 글
| [Algorithm] 스택과 큐_1 (0) | 2022.12.02 |
|---|---|
| [Algorithm] 검색 알고리즘_4 (해시법) (0) | 2022.11.28 |
| [Algorithm] 검색 알고리즘_2 (선형 검색) (0) | 2022.11.27 |
| [Algorithm] 검색 알고리즘_1 (0) | 2022.11.27 |
| [Algorithm] 기본 자료구조와 배열_2 (0) | 2022.11.25 |