728x90
- 일차함수, 기울기와 y 절편
y = ax + b
- x가 일차인 형태 x가 일차로 남으려면 a(기울기)는 0이 아니어야 함.
- 이차함수
y = ax²
- 맨 아래 위치한 최솟값을 찾는 과정이 중요

- 미분 순간 변화율과 기울기
- y = x²에서 x축에 있는 한 점 a에 대응하는 y의 값은 a²
- 이때 a가 오른쪽이나 왼쪽으로 조금씩 이동할 때 y도 조금씩 변화함.
- a가 아주 아주 미세하게 0에 가까울 만큼 움직일 때 y값 역시 매우 미세하게 변화함. 너무 미세해서 방향만 드러내는 정도의 순간적인 변화만 있을 때 이 순간의 변화를 '순간 변화율'이라고 함.
- 이 방향을 따라 직선을 길게 그려주면 그래프오 ㅏ맞닿는 접선이 그려지고, 이 선이 이 점에서의 기울기가 됨.

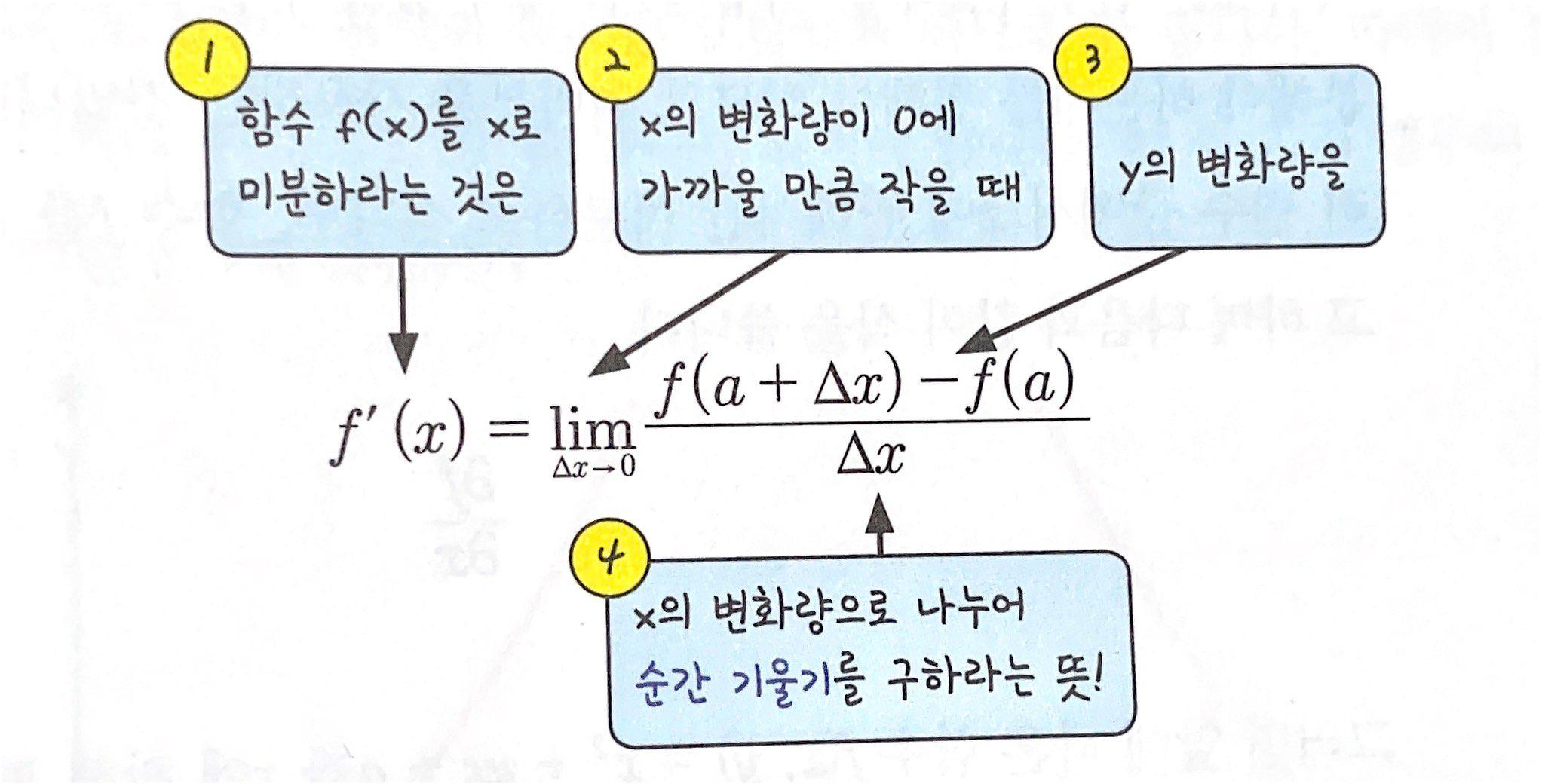
- 미분을 한다 = '순간 변화율'을 구한다
- 어느 순간 어떤 변화가 일어나고 있는지를 숫자로 나타낸 것을 미분 계수라고 함.
- 기울기가 0일 때, x축과 평행한 직선으로 그어질 때가 바로 그래프에서 최솟값이 됨.
- x값과 y값 변화에 따른 직선의 기울기

- 직선 AB의 기울기를 구하는 식

- 함수 f(x) 미분의 공식, 순간 변화율
- 미분의 성질
- f(x) = a에서 a가 상수일 때 미분값은 0입니다.
- f(x) = x일때의 미분 값은 1입니다.
- f(x)= ax에서 a가 상수이며 미분 값은 a입니다.
- f(x) = xⁿ에서 n이 자연수이면 미분값은 nxⁿ-¹입니다.
- 최소 제곱법
- 최소 제곱법은 주어진 x의 값이 하나일 때 적용이 가능함.
- 여러 개의 x가 주어지는 경우 경사하강법을 이용함.
- x의 편차(각 값과 평균과의 차이)를 제곱해서 합한 값을 분모로 놓고, x와 y의 편차를 곱해서 합한 값을 분자로 놓으면 기울기가 나옴.
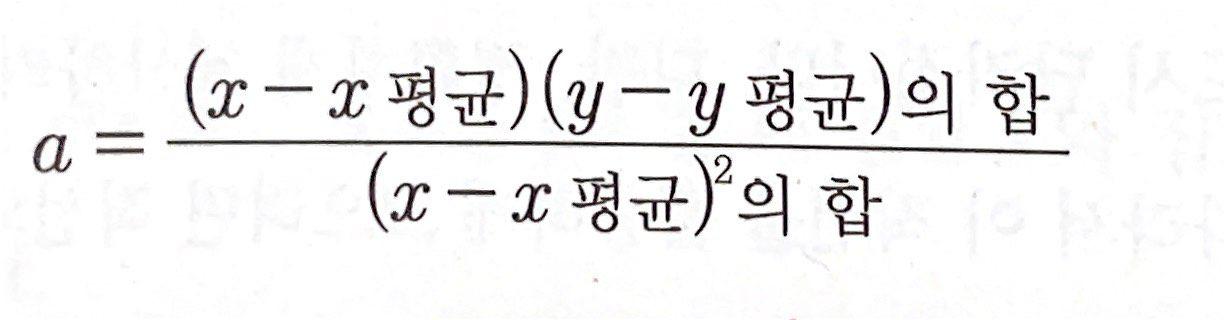
- y 절편 구하는 공식
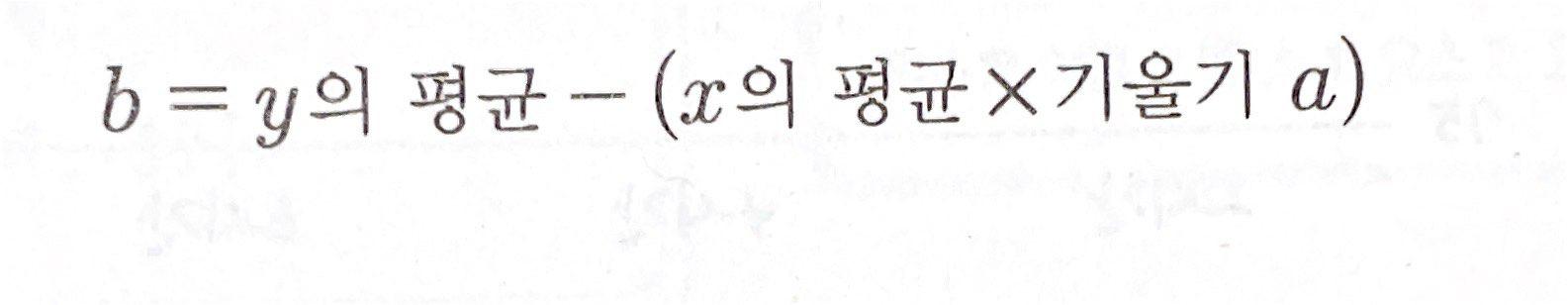
**X를 대입했을 때 나오는 y값을 '예측값'이라고 함.
# 최소 제곱법 코딩으로 구현하기
import numpy as np
x = [2, 4, 6, 8]
y = [81, 93, 91, 97]
mx = np.mean(x)
my = np.mean(y)
# 최소 제곱법 분모 해당하는 값
divisor = sum([(i - mx)**2 for i in x])
# 최소 제곱법 분자에 해당하는 값
def top(x, mx, y, my):
d = 0
for i in range(len(x)):
d += (x[i] - mx) * (y[i] - my)
return d
dividend = top(x, mx, y, my)
print('분모: ',divisor)
print('분자: ',dividend)
# 기울기 구하기
a = dividend / divisor
# y 절편 구하기
b = my - (mx*a)
# 출력으로 확인
print('기울기 a = ',a)
print('y 절편 = ',b)>>>
분모: 20.0
분자: 46.0
기울기 a = 2.3
y 절편 = 79.0
출처: 모두의 딥러닝
notebook ipynb file: https://github.com/heejvely/Deep_learning/blob/main/%EB%AA%A8%EB%91%90%EC%9D%98%EB%94%A5%EB%9F%AC%EB%8B%9D/%EC%B5%9C%EC%86%8C_%EC%A0%9C%EA%B3%B1%EB%B2%95.ipynb
GitHub - heejvely/Deep_learning: deep learning 기초 공부
deep learning 기초 공부. Contribute to heejvely/Deep_learning development by creating an account on GitHub.
github.com
728x90
'Deep Learning' 카테고리의 다른 글
| [Deep Learning] 가중치의 초깃값 (0) | 2022.11.13 |
|---|---|
| [Deep Learning]Optimizer 매개변수 갱신 (2) | 2022.11.13 |
| [Deep Learning]오차역전파의 계산법 (0) | 2022.11.11 |
| [Deep Learning] 오차역전파법 구현(Back Propagation) (0) | 2022.11.07 |
| [Deep Learning]활성화 함수 구현(activation function) (0) | 2022.11.07 |